![]()
One of the most common questions I am asked when flying single line kites is, “How high is it?” I guess it’s the same for most kite flyers. It’s a question that’s not that easy to answer accurately. Most people (including me) just estimate the length of the line and make a guess at the height based on that and the angle the kite is flying at.
David Pelham’s book Kites gives a method that ignores the length of the line, but involves drawing accurate scale diagrams - not so easy to do in the field. My method uses the same principle, but without the drawing.
To calculate the height of your kite you will need:
- a protractor and a plumb line
- a tape measure (or you can pace out the distance)
- a calculator with a tangent function
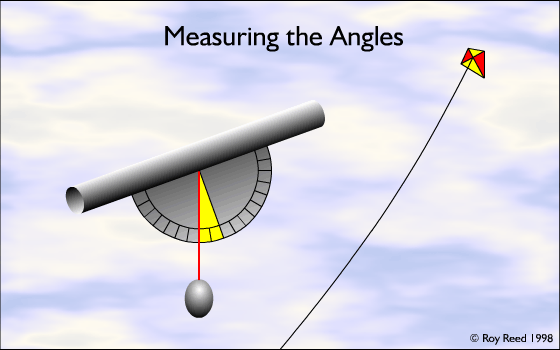
It will help if the protractor has a small tube attached to it to help sighting the kite accurately when you measure its angle above the horizon. The plumb line must be able to swing freely from the centre of the protractor. The angle that you want to measure is the one marked in yellow in the diagram.
Method
You will need to take two angular measurements of the height of the kite above the horizon. The further apart these are, the more accurate your reading will be. These measurements can be taken from anywhere, but for ease of sighting, keep in the same plane as the kite line. The other thing that you will need to know is the distance between the two points where you measured the angles. Once you have these three pieces of information, you have all you need in order to calculate the height of the kite.
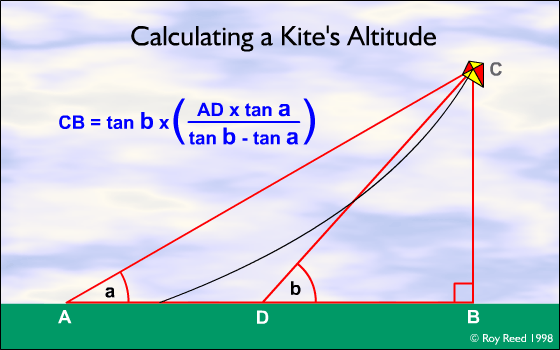
Now comes the maths. In order to calculate the height (distance BC in the diagram) you need to know the distance from point D (the closer of the two measurement points to the kite) to the point directly under the kite, B. Once you know this distance then multiplying this by the tangent of angle b will give you the height.
Here’s an example. Let’s assume that angle a = 48°, angle b = 55° and the distance between them (AD) = 20 metres. Substituting these values into the formula we get:
tan55 × ((tan48 × 20) ÷ (tan55 − tan48))
1.4281 × ((1.1106 × 20) ÷ (1.4281 − 1.1106))
1.4281 × (22.2123 ÷ 0.3175)
1.4281 × 69.96
Using the calculator gives the height of the kite as 99.9, let’s call it 100 metres.
In the diagram, the angles are measured from the ground. In reality you will probably be standing. If you want to be really accurate you need to add the height above the ground that you took the readings, although I doubt if it’s possible to measure the angles accurately enough to make this worthwhile. My guess is that if you are careful taking the measurements you will get an accuracy of ±5%.